Question

Predict if the product will be greater than, less than or equal to the second factor 4/5 x 1 2/5 = y

Answer 1

The product will be less than the second factor.

Explanation:

Given the expression

`(4)/(5)\:* \:1(2)/(5)\:=y`

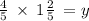
solving to determine the product value

`y=\:(4)/(5)* \:\:1(2)/(5)`

`=(4)/(5)* (7)/(5)`

`\mathrm{Apply\:the\:fraction\:rule}:\quad (a)/(b)* (c)/(d)=(a\:* \:c)/(b\:* \:d)`

`=(4* \:7)/(5* \:5)`

`=(28)/(5* \:5)`

`=(28)/(25)`

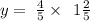
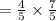
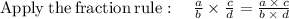
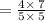
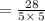
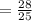
As the value of the second factor is:

`1(2)/(5)=(7)/(5)=1.4`

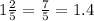
And the product value is:

`y=(28)/(25)=1.12`

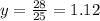
It is clear that the product value 'y = 1.12' is lesser than the second factor value '1.4'.

i.e. 1.12 < 1.4

Thus, the product will be less than the second factor.