Answer: B
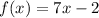 and
and
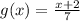
How to solve:
check if the composite functions of f(x) and g(x) are equal to x (this means they are inverses)
f[g(x)] = x
g[f(x)] = x
Explanation:
Checking A.
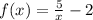
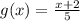
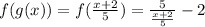
This does not equal x, so we know these are not inverses
Checking B.
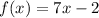
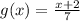
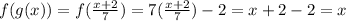
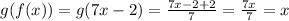
since both f(g(x)) = x and g(f(x)) = x, we can determine that they are inverses of each other.