Question

What is the slope-intercept equation of the line that is perpendicular to y-4=-2/3(x-6) and that passes through (-2, -2)?

Answer 1

The slope-intercept equation is:

`y=(3)/(2)x+1`

Explanation:

Given the equation

`y-4=-(2)/(3)\left(x-6\right)`

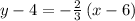
comparing it with the point-slope form of the line equation

`y-y_1=m\left(x-x_1\right)`

where m is the slope

• so the slope of the line is -2/3.

As we know that the slope of the perpendicular line is basically the negative reciprocal of the slope of the line, so

The slope of the perpendicular line will be: 3/2

The point-slope form of the equation of the perpendicular line that goes through (-2, -2) is:

`y-y_1=m\left(x-x_1\right)`

`y-\left(-2\right)=(3)/(2)\left(x-\left(-2\right)\right)`

`y+2=(3)/(2)\left(x+2\right)`

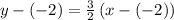
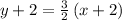
writing the line equation in the slope-intercept form

`y+2=(3)/(2)\left(x+2\right)`

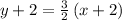
subtract 2 from both sides

`y+2-2=(3)/(2)\left(x+2\right)-2`

`y=(3)/(2)x+1`

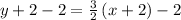
Thus, the slope-intercept equation is:

`y=(3)/(2)x+1`

Here,

As the slope-intercept form is

`y=mx+b`

where m is the slope and b is the y-intercept

so

`y=(3)/(2)x+1`

m=3/2

b = y-intercept = 1

Therefore, the slope-intercept equation is:

`y=(3)/(2)x+1`