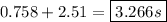Question

PHYSICS, HELP PLZ??!! 100PTS

A ball is thrown from the top of a building
upward at an angle of 48◦
to the horizontal
and with an initial speed of 10 m/s. The
ball is thrown at a height of 28 m above the
ground. calculate how long the ball is in the air until touched the ground, I think is 3.26616298 but is correct :(

Answer 1

Hi there!

We can begin by calculating the time the ball takes to reach the highest point of its trajectory, which can be found using the following:

`t_(max) = (vsin\theta)/(g)`

Where:

tmax = (? sec)

vsinθ = vertical comp. of velocity = 10sin(48) = 7.43 m/s)

g = acceleration due to gravity (9.8 m/s²)

We can solve for this time:

`t_(max) = (7.43)/(9.8) = 0.758 s`

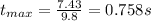
When the ball is at the TOP of its trajectory, its VERTICAL velocity is equivalent to 0 m/s. Thus, we can consider this a free-fall situation.

We must begin by solving for the maximum height reached by the ball using the equation:

`d = y_0 + v_(0y)t + (1)/(2)at^2`

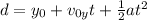
d = displacement (m)

vi = initial velocity (7.43 m/s)

a = acceleration due to gravity

d = displacement (m)

y0 = initial VERTICAL displacement (28m)

Plug in the values:

`d = 28 + 7.43(0.758) + (1)/(2)(-9.8)(0.758^2) = 30.817 m`

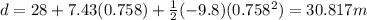
Now, we can use the rearranged kinematic equation:

`t = \sqrt{(2h)/(g)}`

`t = \sqrt{(2(30.817))/(9.8)} = 2.51 s`

Add the two times together:

`0.758 + 2.51 = \boxed{3.266 s}`

Answer 2

t = 3.27 s (2 d.p.)

Step-by-step explanation:

Use the Constant Acceleration Equations where:

• s = displacement in meters
• u = initial speed in m/s
• v = final speed in m/s
• a = acceleration in m/s²
• t = time in s (seconds)

As the projectile is modeled as moving only under the influence of gravity, the only acceleration the projectile will experience will be acceleration due to gravity (g = 9.8 m/s²). Acceleration due to gravity acts vertically downwards, so will only affect the vertical component of the projectile's velocity.

To find the time it takes for the ball to touch the ground, resolve vertically, taking up as positive:

Given:

• s = -28 m
• u = 10 sin 48°
• a = -9.8
• t = t

`\begin{aligned}\textsf{Using} \quad s & =ut+(1)/(2)at^2\\\implies -28 & = (10 \sin 48^(\circ))t+(1)/(2)(-9.8)t^2\end{aligned}`

Rearrange the equation to equal zero:

`\implies 4.9t^2-(10 \sin 48^(\circ))t-28 =0`

Quadratic Formula

`x=(-b \pm √(b^2-4ac) )/(2a)\quad\textsf{when }\:ax^2+bx+c=0`

Use the quadratic equation to solve for t:

`\implies t=\frac{-(-10 \sin 48^(\circ)) \pm \sqrt{(-10 \sin 48^(\circ))^2-4(4.9)(-28)} }{2(4.9)}`

`\implies t=3.266162987, -1.749540894`

As time is positive,

`\implies t=3.266162987...`

`\implies t=3.27 \: \sf s \: \:(2\:d.p.)`