If we evaluate at infinity, we have:
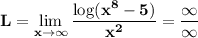
However, the infinity of the denominator has a higher order. Therefore, we can conclude that
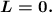
However, proving that the limit is 0 without using L'Hopital or the "order" criterion is complicated. To do so, let us denote:
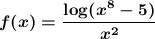
To find the limit, we must look for two functions h(x) and g(x) such that h(x)≤ f(x)≤ g(x) and

If we find these functions, then we can conclude that
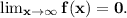
First, let's note that when x⁸ - 5 > 1, then log(x⁸ - 5) > 0 (and this is true when x is large). Likewise, we have that x² > 0 for x > 0. Therefore, we have:
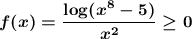
when x "is big enough". Thus, we have h(x) = 0 where it is clear that
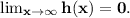
To find the second function, let's first note that \log is an increasing function, so since x⁸ ≥ x⁸ - 5, then log(x⁸) ≥ log(x⁸ - 5). So we have to
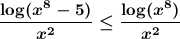
now, if we take y = e^y, then we can write
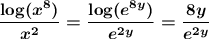
A very important property about the exponential function is
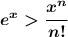
For any n
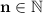 and x > 0. If we take n = 2, then we have
and x > 0. If we take n = 2, then we have
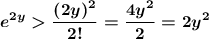
From this it follows that
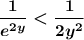
Therefore, we have to
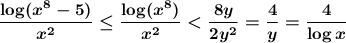
yes,
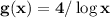 where
where
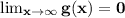 . Also,
. Also,
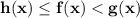 . Therefore,
. Therefore,
 .
.
