Question

Graph the rational function f of x equals quantity 2 times x minus 3 end quantity divided by quantity x plus 4 end quantity.

A rational function is graphed in the first quadrant, and in the third and fourth quadrant is another piece of the graph. The graph approaches an imaginary horizontal line at y equals 2 and approaches an imaginary vertical line at x equals 4.

A rational function is graphed in the second quadrant, and in the first and third quadrant is another piece of the graph. The graph approaches an imaginary horizontal line at y equals 2 and approaches an imaginary vertical line at x equals negative 4.

A rational function is graphed in the second quadrant, and in the fourth quadrant is another piece of the graph. The graph approaches an imaginary horizontal line at y equals 2 and approaches an imaginary vertical line at x equals 1.

A rational function is graphed in the first quadrant, and in the third quadrant is another piece of the graph. The graph approaches an imaginary horizontal line at y equals 2 and approaches an imaginary vertical line at x equals negative 1.

Answer 1

A The answer is A

Explanation:

Answer 2

A graph of the function
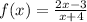`f(x)=(2x-3)/(x+4)` is: B. A rational function is graphed in the second quadrant, and in the first and third quadrant is another piece of the graph. The graph approaches an imaginary horizontal line at y equals 2 and approaches an imaginary vertical line at x equals negative 4.

In Mathematics and Euclidean Geometry, a rational function is a type of function which is expressed as a fraction that is composed of two main parts and these include the following:

• Numerator
• Denominator

Based on the information provided above, we would translate the text into a rational function;

`f(x)=(2x-3)/(x+4)`

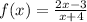
In order to graph any rational function, you should determine the values for which it is undefined. This ultimately implies that, a function is considered as undefined when the value of the denominator is equal to zero, which represents vertical asymptote lines;

x + 4 = 0

x = 0 - 4

x = -4 (vertical asymptote)

Horizontal asymptote: y = 2 (since the degree of the denominator is equal to that of the numerator).