Answer:
95% confidence interval for the mean time spent on housework per week by all married women.
( 26.66 , 32.94)
Explanation:
Step(i):-
Given random sample size 'n' = 20
Mean of the sample (x⁻ ) = 29.8 hours
Standard deviation of the sample (S) = 6.7
Given Margin of error = 3.14
Step(ii):-
95% confidence interval for the mean is determined by
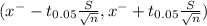
We know that margin of error is determined by
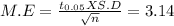
Now 95% confidence interval for the mean time spent on housework per week by all married women.
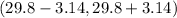
( 26.66 , 32.94)