Question

A line passes through point A (14,21). A second point on the line has an x-value that is 125% of the x-value of point A and a y-value

that is 75% of the y-value of point A. Use point A to write an equation of the line in point-slope form.

?:(

Answer 1

The equation of the line in point-slope form is
`y-21 = - (3)/(2)\cdot (x-14)`.

Explanation:

According to the statement, let
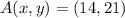`A(x,y) = (14,21)` and
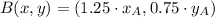`B(x,y) = (1.25\cdot x_(A),0.75\cdot y_(A))`. The equation of the line in point-slope form is defined by the following formula:

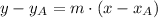`y-y_(A) = m\cdot (x-x_(A))` (1)

Where:

`x_(A)`,
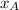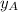`y_(A)` - Coordinates of the point A, dimensionless.

`m` - Slope, dimensionless.

`x` - Independent variable, dimensionless.

`y` - Dependent variable, dimensionless.

In addition, the slope of the line is defined by:

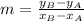`m = (y_(B)-y_(A))/(x_(B)-x_(A))` (2)

If we know that
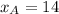`x_(A) = 14` and
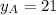`y_(A) = 21`, then the equation of the line in point-slope form is:

`x_(B) = 1.25\cdot (14)`

`x_(B) = 17.5`

`y_(B) = 0.75\cdot (21)`

`y_(B) = 15.75`

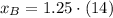
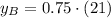
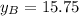
From (2):

`m = (15.75-21)/(17.5-14)`

`m = -(3)/(2)`

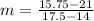
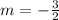
By (1):

`y-21 = - (3)/(2)\cdot (x-14)`

The equation of the line in point-slope form is
`y-21 = - (3)/(2)\cdot (x-14)`.