Question

The length of each side of an equilateral triangle is increased by 20%, resulting in triangle ABC. If the length of each side of the original equilateral is decreased by 20%, resulting in triangle DEF, how much greater is the area of triangle ABC than the area of triangle DEF?

Answer 1

Answer: Area of ΔABC is 2.25x the area of ΔDEF.

Explanation: Because equilateral triangle has 3 equal sides, area is calculated as

`A=(√(3) )/(4) a^(2)`

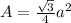
with a as side of the triangle.

Triangle ABC is 20% bigger than the original, which means its side (a₁) measures, compared to the original:

a₁ = 1.2a

Then, its area is

`A_(1)=(√(3) )/(4)(1.2a)^(2)`

`A_(1)=(√(3) )/(4)1.44a^(2)`

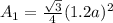
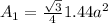
Triangle DEF is 20% smaller than the original, which means its side is:

a₂ = 0.8a

So, area is

`A_(2)=(√(3) )/(4) (0.8a)^(2)`

`A_(2)=(√(3) )/(4) 0.64a^(2)`

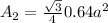
Now, comparing areas:

`(A_(1))/(A_(2))= ((√(3).1.44a^(2) )/(4))((4)/(√(3).0.64a^(2) ) )`

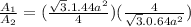
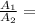`(A_(1))/(A_(2)) =` 2.25

The area of ΔABC is 2.25x greater than the area of ΔDEF.