Question

footpath is to be constructed in a park in the shape of a parallelogram. When a coordinate plane is laid over a map of the park, the vertices of the footpath are (−4, 2), (8, 2), (11, 7), and (−1, 7).

Answer 1

35.7

Explanation:

Step one

Given the coordinates

ABCD with vertices A(−4, 2), B(8,2), C(11, 7), and D(-1, 7).

AB=(−4, 2), (8,2)

BC=(8,2), (11, 7)

CD=(11, 7),(-1, 7)

DA=(-1, 7),(-4,2)

The distance between points AB=

`AB= \sqrt (x_2-x_1)^2+(y_2-y_1)^2`

`AB= \sqrt (8+4)^2+(2-2)^2\\\\AB= \sqrt 12^2+(0)^2\\\\AB= \sqrt144\\\\AB=12`

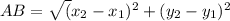
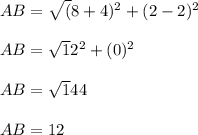
The distance between points BC=

`BC= \sqrt (11-8)^2+(7-2)^2\\\\BC= \sqrt 3^2+(5)^2\\\\BC= \sqrt34\\\\BC=5.8`

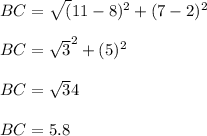
The distance between points CD

`CD= \sqrt (-1-11)^2+(7-7)^2\\\\CD= \sqrt -12^2+(0)^2\\\\CD= \sqrt144\\\\CD=12`

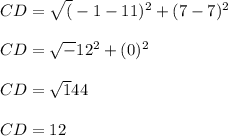
The distance between points DA

`DA= \sqrt (-4+1)^2+(2-7)^2\\\\DA= \sqrt -3^2+(-5)^2\\\\DA= \sqrt34\\\\DA=5.8`

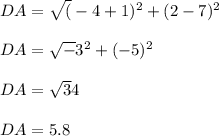
Hence the perimeter of the footpath= 12+5.8+12+5.8

=35.7