Question

A mixture is prepared using 27.00 mL of a 0.0758 M weak base (pKa=4.594) , 27.00 mL of a 0.0553 M weak acid (pKa=3.235) and 1.00 mL of 1.25×10−4 M HIn and then diluting to 100.0 mL, where HIn is the protonated indicator. The absorbance measured at 550 nm in a 5.000 cm cell was 0.1102 . The molar absorptivity (????) values for HIn and its deprotonated form In− at 550 nm are 2.26×104 M−1cm−1 and 1.53×104 M−1cm−1 , respectively. What is the pH of the solution?

Answer 1

pH = 4.164

Step-by-step explanation:

The first process is to find the initial moles for the base (B) & the acid (HA)

i.e.

`= (27 mL * 0.0758 \ moles \ \ of \ B)/(1000 \ mL)`

`=0.0020466`

`\simeq 2.047* 10^(-3) \ moles \ of \ B`

`= (27 mL * 0.0553 \ moles \ \ of \ HA)/(1000 \ mL)`

`=0.0014931`

`\simeq 1.493* 10^(-3) \ moles \ of \ HA`

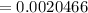
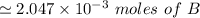
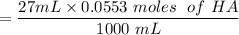
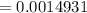
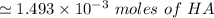
The acid with base reaction is expressed as;

HA + B → A⁻ + HB⁺

to 1.493 × 10⁻³ 2.047 × 10⁻³ - -

- 1.493 × 10⁻³ 1.493 × 10⁻³ 1.493 × 10⁻³ 1.493 × 10⁻³

0 5.54 × 10⁻⁴ 1.493 × 10⁻³ 1.493 × 10⁻³

From observation; both the acid & base weak

Given that:

The pKa for base = 4.594

The pKa for acid = 3.235

Recall that;

pKa = -log Ka

So; Ka =
`\mathbf{10^(-Ka)}`

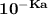
By applying this:

For Base; Ka =
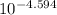`10^(-4.594)` = 2.5468 × 10⁻⁵

For Acid: Ka =
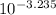`10^( -3.235)` = 5.821 × 10⁻⁴

After the reaction; we have the base with its conjugate acid & conjugate base of acid; Thus, since the conjugate acid of the base possesses a higher value of K, it is likely it would be the one to define the pH of the solution.

By analyzing the system, we have:

HB⁺ + H₂O ↔ B + H₃O⁺

`(1.493* 10^(-3))/(0.1 \ L)`
`(5.54* 10^(-4))/(0.1 \ L)`

to 0.01493 M 0.00554 M

- x x x

0.01493 - x 0.00554 - x x

Thus;

`2.5468 * 10^(-5) = ((0.00554 -x)* x)/((0.01493-x))`

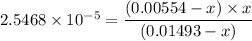
Using the common ion effect;

0.00554 - x
`\simeq` 0.00554 &

0.01493 - x
`\simeq` 0.01493

∴

`x = (2.5468 * 10^(-5) * 0.01493)/(0.00554)`

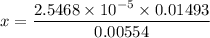
x = [H₃O⁺] = 6.8635 × 10⁻⁵

∴

pH = -log(6.8635 × 10⁻⁵)

pH = 4.164