Question

Data on investments in the​ high-tech industry by venture capitalists are compiled by a corporation. A random sample of 18​venture-capital investments in a certain business sector yielded the accompanying​ data, in millions of dollars. Determine and interpret a 95​%confidence interval for the mean​ amount, mu​,of all​ venture-capital investments in this business sector. Assume that the population standard deviation is ​$1.70million.​ (Note: The sum of the data is ​$102.52​million.)

Answer 1

$4.911 million or $6.481 million

Thus, we are 95% confident that the mean amount of all venture-capital investments in the high-tech industry is somewhere between $4.911 million and $6.481 million.

Explanation:

Given that:

sample size n = 18

standard deviation σ = 1.70

confidence interval = 95%

Sample mean
`\overline x =( \sum x )/(n)`

`\overline x =( 102.52 )/(18)`

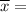`\overline x =` 5.696

The level of significance = 1 - C.I

= 1 - 0.95

= 0.05

The critical value of
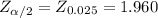`Z_(\alpha/2) = Z_(0.025) = 1.960` from the Z tables

The 95% C.I for the mean is;

`= \overline x \pm Z_(\alpha/2) * (\sigma)/(√(n))`

`=5.696 \pm 1.960 * (1.70)/(√(18))`

`=5.696 \pm 1.960 * (1.70)/(4.243)`

`=5.696 \pm 1.960 * 0.4007`

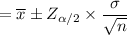
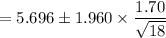
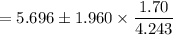
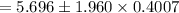
= 5.696 ± 0.785372

= (5.696 - 0.785372 , 5.696 + 0.785372 )

= ( 4.910628 , 6.481372 )

≅ $4.911 million or $6.481 million.

Thus, we are 95% confident that the mean amount of all venture-capital investments in the high-tech industry is somewhere between $4.911 million and $6.481 million.