Answer:
The sample statistics follows a standard normal distribution since the sample size are large enough.
Explanation:
Given that:
First population:
Sample size
 = 49
= 49
Population standard deviation
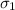 = 3
= 3
Sample mean
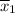 = 10
= 10
Second population:
Sample size
 = 64
= 64
Population standard deviation
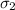 = 4
= 4
Sample mean
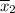 = 12
= 12
The sample statistics follows a standard normal distribution since the sample size are large enough.
The null and alternative hypotheses can be computed as:
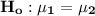
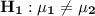
Level of significance = 0.01
Using the Z-test statistics;
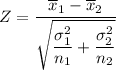
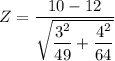
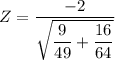

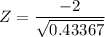
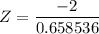
Z = - 3.037
Z
 - 3.04
- 3.04
The P-value = 2P (z < -3.04)
From the z tables
= 2 × (0.00118)
= 0.00236
Thus, since P-value is less than the level of significance, we fail to reject the null hypotheses
