Question

A 782-kg satellite is in a circular orbit about Earth at a height above Earth equal to Earth's mean radius. (a) Find the satellite's orbital speed. 9.82278e7 Incorrect: Your answer is incorrect. Your response differs significantly from the correct answer. Rework your solution from the beginning and check each step carefully. m/s (b) Find the period of its revolution. h (c) Find the gravitational force acting on it.

Answer 1

a) v = 5.59x10³ m/s

b) T = 4 h

c) F = 1.92x10³ N

Step-by-step explanation:

a) We can find the satellite's orbital speed by equating the centripetal force and the gravitation force as follows:

`F_(c) = F_(G)`

`(mv^(2))/(r + h) = (GMm)/((r + h)^(2))`

`v = \sqrt{(gr^(2))/(r+h)`

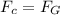
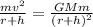
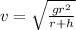
Where:

g is the gravity = 9.81 m/s²

r: is the Earth's radius = 6371 km

h: is the satellite's height = r = 6371 km

`v = \sqrt{(gr^(2))/(2r)} = \sqrt{(gr)/(2)} = \sqrt{(9.81 m/s^(2)*6.371 \cdot 10^(6) m)/(2)} = 5.59 \cdot 10^(3) m/s`

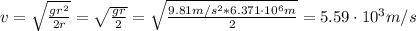
b) The period of its revolution is:

`T = (2\pi)/(\omega) = (2\pi (r + h))/(v) = (2\pi (2*6.371 \cdot 10^(6) m))/(5.59 \cdot 10^(3) m/s) = 14322.07 s = 4 h`

c) The gravitational force acting on it is given by:

`F = (GMm)/((r + h)^(2))`

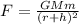
Where:

M is the Earth's mass = 5.97x10²⁴ kg

m is the satellite's mass = 782 kg

G is the gravitational constant = 6.67x10⁻¹¹ Nm²kg⁻²

`F = (GMm)/((r + h)^(2)) = (6.67 \cdot 10^(-11) Nm^(2)kg^(-2)*5.97 \cdot 10^(24) kg*782 kg)/((2*6.371 \cdot 10^(6) m)^(2)) = 1.92 \cdot 10^(3) N`

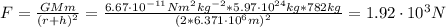
I hope it helps you!