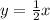Question

Find the equation of a line that passes through the points (-4, -2) and (6, 3).

Answer 1

`y=(1)/(2) x`

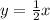
Explanation:

The equation of a line through two points can usually (except when the line is a vertical line) be written in slope intercept form,
`y=mx+b` , where "m" is the slope of the line, and "b" is the y-intercept of the line.

General outline

1. Find the slope
2. Find the y-intercept

Step 1. Find the slope

To find "m", use the formula for slope:

`m=(y_2-y_1)/(x_2-x_1)`

`m=((3)-(-2))/((6)-(-4))`

`m=(3+2)/(6+4)`

`m=(5)/(10)`

`m=(1)/(2)`

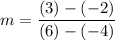
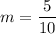
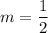
So, the slope is 1/2 and we know that the equation for the line that passes through these two points should look like:
`y=(1)/(2) x+b`

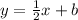
Step 2. Find the y-intercept

To find "b", substitute one of the known points, and solve for "b":

`y=(1)/(2) x+b`

`(3)=(1)/(2) (6)+b`

`3=3+b`

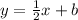
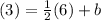
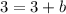
Subtracting 3 from both sides to isolate the "b"...

`(3)-3=(3+b)-3`

`0=b`

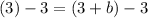
So, the y-intercept is 0. Substituting into our line equation,
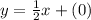`y=(1)/(2) x+(0)` which simplifies to
`y=(1)/(2) x`