Question

A principal of ​$6000 is invested in an account paying an annual rate of 5​%. Find the amount in the account after 4 years if the account is compounded​ semiannually, quarterly, and monthly. ​(a) The amount in the account after 4 years if the account is compounded semiannually is ​$ nothing. ​(Round to the nearest​ cent.)

Answer 1

Given :

Principal amount deposited, P = $ 6000

Rate of interest, r = 5%

Number of years, t = 4 years

When the deposited amount is compounded semiannually, i.e. n = 2

Therefore,

Future value,

`$FV = P\left( 1 +(r)/(n)\right)^(nt)$`

`$FV = 6000\left( 1 +(0.05)/(2)\right)^(2 * 4)$`

`$FV = 6000 * (1.025)^8$`

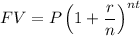
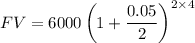
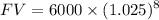
= 6000 x 1.2184

= 7310.4

Therefore, after 4 years there will be $ 7310.4 in the amount when compounded semi annually.

When the deposited amount is compounded quarterly, i.e. n = 4

Therefore,

Future value,

`$FV = P\left( 1 +(r)/(n)\right)^(nt)$`

`$FV = 6000\left( 1 +(0.05)/(4)\right)^(4 * 4)$`

`$FV = 6000 * (1.0125)^(16)$`

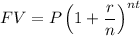
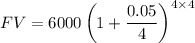
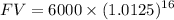
= 6000 x 1.219889

= 7319.334

Therefore, after 4 years there will be $ 7319.334 in the amount when compounded quarterly.

When the deposited amount is compounded monthly, i.e. n = 12

Therefore,

Future value,

`$FV = P\left( 1 +(r)/(n)\right)^(nt)$`

`$FV = 6000\left( 1 +(0.05)/(12)\right)^(12 * 4)$`

`$FV = 6000 * (1.0041667)^(48)$`

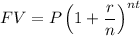
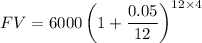
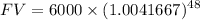
= 6000 x 1.22089

= 7325.34

Therefore, after 4 years there will be $ 7325.34 in the amount when compounded monthly.