Question

Assume that, when we walk, in addition to a fluctuating vertical force, we exert a periodic lateral force of amplitude 25 NN at a frequency of about 1 HzHz. Given that the mass of the bridge is about 2000 kgkg per linear meter, how many people were walking along the 144-mm-long central span of the bridge at one time, when an oscillation amplitude of 75 mmmm was observed in that section of the bridge

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

Step-by-step explanation:

From the question we are told

The amplitude of the lateral force is
`F = 25 \ N`

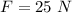
The frequency is
`f = 1 \ Hz`

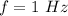
The mass of the bridge per unit length is
`\mu = 2000 \ kg /m`

The length of the central span is
`d = 144 m`

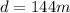
The oscillation amplitude of the section considered at the time considered is
`A = 75 \ mm = 0.075 \ m`

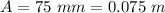
The time taken for the undriven oscillation to decay to
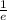`(1)/(e)` of its original value is t = 6T

Generally the mass of the section considered is mathematically represented as

`m = \mu * d`

=>
`m = 2000 * 144`

=>
`m = 288000 \ kg`

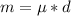
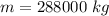
Generally the oscillation amplitude of the section after a time period t is mathematically represented as

`A(t) = A_o e^{-(bt)/(2m) }`

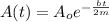
Here b is the damping constant and the
`A_o` is the amplitude of the section when it was undriven

So from the question

`(A_o)/(e) = A_o e^{-(b6T)/(2m) }`

=>
`(1)/(e) =e^{-(b6T)/(2m) }`

=>
`e^(-1) =e^{-(b6T)/(2m) }`

=>
`-(3T b)/(m) = -1`

=>
`b = (m)/(3T)`

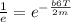
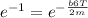
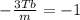
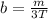
Generally the amplitude of the section considered is mathematically represented as

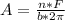
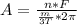
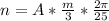
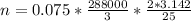
`A = (n * F )/( b * 2 \pi )`

=>
`A = (n * F )/( (m)/(3T) * 2 \pi )`

=>
`n = A * (m)/(3) * (2\pi)/(25)`

=>
`n = 0.075 * (288000)/(3) * (2* 3.142 )/(25)`

=>
`n = 1810 \ people`