Question

A thin, uniform stick of mass M and length L is at rest on a flat, frictionless surface to which one end of it is pinned. A small mass m traveling at speed v collides with and attaches to the stick at a distance 2L/3 away from the end through which it is pinned to the surface. (a) Find an expression for the moment of inertia of the stick mass object after the collision. (b) Find an expression for the final angular speed of the combined object

Answer 1

a) I = (
`(M)/(3)` +
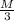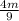`(4m)/(9)`) L² , b) w = (\frac{27 M}{18 m} + 2)⁻¹ Lv₀

Step-by-step explanation:

a) The moment of inertia is a scalar that represents the inertia in circular motion, therefore it is an additive quantity.

The moment of inertia of a rod held at one end is

I₁ = 1/3 M L²

The moment of inertia of the mass at y = L

I₂ = m y²

The total inertia method

I = I₁ + I₂

I = \frac{1}{3} M L² + m (\frac{2}{3} L)²

I = (
`(M)/(3)` +
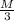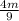`(4m)/(9)` ) L²

b) The conservation of angular momentum, where the system is formed by the masses and the bar, in such a way that all the forces during the collision are internal.

Initial instant. Before the crash

L₀ = I₂ w₀

angular and linear velocity are related

w₀ = y v₀

w₀ =
`(2)/(3)`L v₀

L₀ = I₂ y v₀

Final moment. After the crash

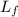`L_(f)` = I w

how angular momentum is conserved

L₀ = L_{f}

I₂ y v₀ = I w

substitute

m (
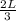`(2L)/(3)`)² (\frac{2L}{3} v₀ = (
`(M)/(3)` +
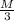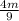`(4m)/(9)` ) L² w

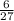`(6)/(27)` m L³ v₀ = (
`(M)/(3)` +
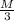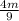`(4m)/(9)` ) L² w

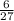`(6)/(27)` m L v₀ = (
`(M)/(3)` +
`(4m)/(9)` ) w

L v₀ =
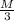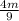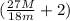`((27 M)/(18 m) + 2)` w

w = (\frac{27 M}{18 m} + 2)⁻¹ Lv₀