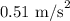Answer:
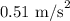
Step-by-step explanation:
t = Time taken
g = Acceleration due to gravity =
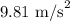
r = Radius of track = 0.355 km
Displacement in
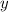 direction is 3 m
direction is 3 m
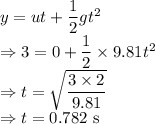
Displacement in
 direction
direction
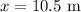
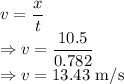
Centripetal acceleration is given by
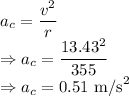
The minimum centripetal acceleration the truck must have is