Answer:
Para x=0:
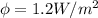
Para x=30 cm:
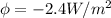
Step-by-step explanation
Podemos utilizar la ley de Fourier par determinar el flujo de calor:
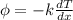 (1)
(1)
Por lo tanto debemos encontrar la derivada de T(x) con respecto a x primero.
Usando la ley de potencia para la derivda, tenemos:
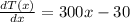
Remplezando esta derivada en (1):
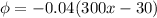
Para x=0:
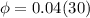
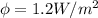
Para x=30 cm:
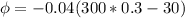
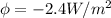
Espero que te haya ayudado!