Answer:
a) La piedra es lanzada desde una altura de 0,785 metros.
b) La piedra es lanzada con una velocidad inicial de 6,25 metros por segundo.
Step-by-step explanation:
a) Dado que la piedra es lanzada horizontalmente, tenemos que la piedra experimenta un movimiento horizontal a velocidad constante y uno vertical uniformemente acelerado debido a la gravedad. La altura de la que fue lanzada la piedra se puede determinar mediante la siguiente ecuación cinemática:
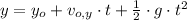 (1)
(1)
Donde:
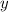 - Altura final, medida en metros.
- Altura final, medida en metros.
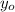 - Altura inicial, medida en metros.
- Altura inicial, medida en metros.
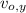 - Componente vertical de la velocidad inicial, medida en metros por segundo.
- Componente vertical de la velocidad inicial, medida en metros por segundo.
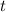 - Tiempo, medido en segundos.
- Tiempo, medido en segundos.
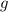 - Aceleración gravitacional, medida en metros por segundo cuadrado.
- Aceleración gravitacional, medida en metros por segundo cuadrado.
Si sabemos que
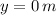 ,
,
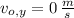 ,
,
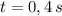 y
y
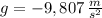 , entonces la altura inicial de la piedra es:
, entonces la altura inicial de la piedra es:
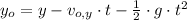
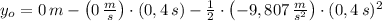
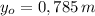
La piedra es lanzada desde una altura de 0,785 metros.
b) Ahora, obtenemos el componente horizontal de la velocidad inicial a partir de la siguiente ecuación cinemática:
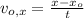 (2)
(2)
Donde:
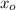 ,
,
 - Posiciones horizontales iniciales y finales, medidas en metros.
- Posiciones horizontales iniciales y finales, medidas en metros.
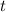 - Tiempo, medido en segundos.
- Tiempo, medido en segundos.
Si tenemos que
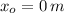 ,
,
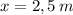 y
y
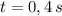 , entonces el componente horizontal de la velocidad inicial es:
, entonces el componente horizontal de la velocidad inicial es:
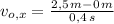
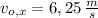
La piedra es lanzada con una velocidad inicial de 6,25 metros por segundo.