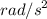Question

- During a certain period, the angular position of a rotating object is given by: = − + , where  is in radian and t is in seconds. Determine the angular position, angular speed, and angular acceleration of the rotating object at = Sec.

Answer 1

The question is not complete. The complete question is :

During a certain period of time, the angular position of a rotating object is given by
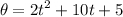`$\theta =2t^2 +10t+5$`, where θ is in radians and t is in seconds. Determine the angular position, angular speed, and angular acceleration of the door (a) at t = 0.00 seconds, (b) at t = 3.00 seconds.

Solution :

Given :

Displacement or angular position of the object,
`$\theta =2t^2 +10t+5$`

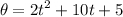
∴ Angular speed is
`$\omega = (d \theta)/(dt)$`

ω = 10 + 4t

And angular acceleration is
`$\alpha = (d \omega)/(dt)$`

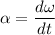
α = 4

a). At time, t = 0.00 seconds :

Angular displacement is
`$\theta =2t^2 +10t+5$`

`$\theta =2(0)^2 +10(0)+5$`

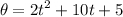
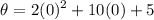
= 5 rad

Angular speed is ω = 10 + 4t

ω = 10 + 4(0)

= 10 rad/s

Angular acceleration is α = 4
`$rad/s^2$`

b). At time, t = 3.00 seconds :

Angular displacement is
`$\theta =2t^2 +10t+5$`

`$\theta =2(3)^2 +10(3)+5$`

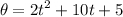
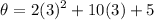
= 53 rad

Angular speed is ω = 10 + 4t

ω = 10 + 4(3)

= 22 rad/s

Angular acceleration is α = 4
`$rad/s^2$`