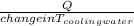Answer:
Q = [ mCp ( ΔT) ]
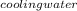
(ΔT)
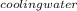 and Q is given
and Q is given
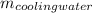 =
=
![(Q)/(Cp[ T_(out) - T_(in) ] )](https://img.qammunity.org/2021/formulas/engineering/college/jy8qzr9c4l6p8bjuwf2jh6no1d3qhb3d2n.png)
next the rate of condensation of the steam
Q = [ m
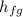 ]
]
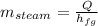
Total resistance of the condenser is
R =
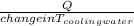
Step-by-step explanation:
How will the rate of condensation of the steam and the mass flow rate of the cooling water can be determined
Q = [ mCp ( ΔT) ]
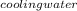
(ΔT)
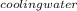 and Q is given
and Q is given
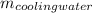 =
=
![(Q)/(Cp[ T_(out) - T_(in) ] )](https://img.qammunity.org/2021/formulas/engineering/college/jy8qzr9c4l6p8bjuwf2jh6no1d3qhb3d2n.png)
next the rate of condensation of the steam
Q = [ m
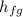 ]
]
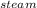
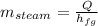
Total resistance of the condenser is
R =