Question

Consider a car engine running at constantspeed. That is, the crankshaft of the en-gine rotates at constant angular velocity whileeach piston moves back-and-forth in its cylin-der according to the rules of simple harmonicmotion.2030 rpm6.95 cmSuppose the two extremal positionsxmaxandxminof a piston are 6.95 cm from eachother.When the crankshaft of the engine rotatesat 2030 rpm (revolutions per minute), what isthe maximal speed|v|maxof the piston?Answer in units of m/s.

Answer 1

The value is
`|v| = 7.39 \ m/s`

Step-by-step explanation:

From the question we are told that

The angular speed is
`w = 2030 \ rpm = (2030 * 2 * \pi )/( 60) = 212.61 \ rad/s`

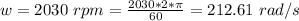
The distance between the minimum and maximum external position is
`d = 6.95 \ cm = 0.0695 \ m`

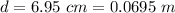
Generally the amplitude of the crank shaft is mathematically represented as

`A = (d)/(2)`

=>
`A = (0.0695)/(2)`

=>
`A = 0.03475 \ m`

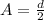
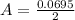
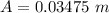
Generally the maximum speed of the piston is mathematically represented as

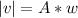
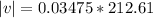
`|v| = A * w`

=>
`|v| = 0.03475 * 212.61`

=>
`|v| = 7.39 \ m/s`