Answer:
To raise the mass to an altitude of 12,000 Km 2E joules are required.
Step-by-step explanation:
Gravitational Potential Energy
It's the energy stored in an object because of its vertical position or height in a gravitational field.
It can be calculated with the equation:
U=m.g.h
Where:
m = mass of the object
h = height with respect to a fixed reference
g = acceleration of gravity, or
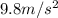 .
.
If a mass has a height h1, its potential energy is
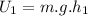
If a mass has a height h2, its potential energy is
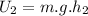
The ratio of both potential energies is:
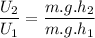
Simplifying:
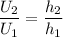
Solving for U2:
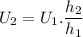
Since U1=E:
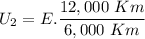

To raise the mass to an altitude of 12,000 Km 2E joules are required.