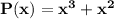Question

Write a polynomial in standard form with
zeros of 0 with a multiplicity of 2, and -1

Answer 1

`P(x)=x^3+x^2`

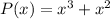
Explanation:

Polynomials

Given the roots or zeros of a polynomial as x1, x2, x3, ...xn and the leading factor a, the polynomial can be expressed as:

`P(x)=a(x-x_1)(x-x_2)(x-x_3)...(x-x_n)`

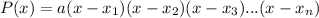
We are given the zeros of a polynomial as x1=0, x2=0 (multiplicity or zeros), and x3=-1, thus the polynomial is:

`P(x)=a(x-0)(x-0)(x+1)`

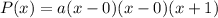
Operating:

`P(x)=a.x.x(x+1)`

`P(x)=ax^2(x+1)`

`P(x)=ax^3+ax^2`

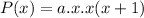
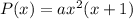
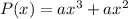
Assuming a=1, the polynomial is

`\mathbf{P(x)=x^3+x^2}`