Answer:
- The equation connecting c and d is: c = kd
- The value of c when d=8 is: 48
- The value of d when c=54 is: 9
Explanation:
Proportion can be defined as the effect of changing one quantity on the other.
Given that
‘c’ is directly proportional to‘d’
It can mathematically be written as:
c∝d
A constant is introduced in the equation when the proportionality symbol will be removed. The constant is called constant of proportionality
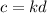
Given that
c = 24 when d = 4
Putting the values
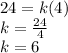
Putting the value of k
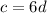
Putting d = 8
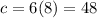
Putting c = 54
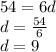
Hence,
- The equation connecting c and d is: c = kd
- The value of c when d=8 is: 48
- The value of d when c=54 is: 9