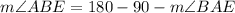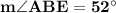1 Answer

Son · Answer 1 · 2021-03-21T00:06:58+0000

Answer:

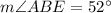
$m\angle ABE=52^\circ$

Explanation:

Angles and Lines

The figure shows a kite ABCD where the following data is given:

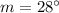
$m\BAE=28^\circ$

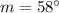
$m\BCE=58^\circ$

We also know

$BC\cong CD$

$AB\cong AD$

Since triangle BCD is isosceles, it follows that:

$m\angle CBE=m\angle CDE$

And triangles BCD and DCE are congruent.

Thus:

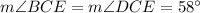
$m\angle BCE=m\angle DCE=58^\circ$

And also:

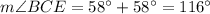
$m\angle BCE=58^\circ+58^\circ=116^\circ$

Since the sum of internal angles of BCD is 180°

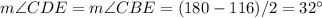
$m\angle CDE=m\angle CBE= ( 180 - 116 ) / 2=32^\circ$

The sum of angles of triangle CDE is 180°, thus

$m\angle CED=180^\circ - 32^\circ - 58^\circ = 90^\circ$

Angles CED and BEA are vertical (opposite), thus:

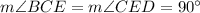
$m\angle BCE=m\angle CED= 90^\circ$

Finally, since the sum of the angles of triangle ABE is 180°

$m\angle ABE= 180 - 90 - m\angle BAE$

$m\angle ABE= 180^\circ - 90^\circ - 28^\circ = 52^\circ$

$\mathbf{m\angle ABE=52^\circ}$

Please log in or register to add a comment.