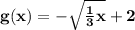Question

Help me please .....

Answer 1

the transformed function will be:
`\mathbf{g(x)=-\sqrt{(1)/(3) x}+2}`

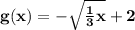
Explanation:

We need to transform
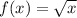`f(x)=√(x)` into g(x) using following translations

1) reflection in the x-axis

The reflection across x-axis will be:

`g(x)=-√(x)`

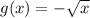
2) Horizontal shrink by a factor of 1/3

The horizontal shrink by a factor of 1/3 will make the function g(x)

`g(x)=-\sqrt{(1)/(3) x}`

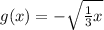
3) Vertical translation up 2 units

The vertical translation up 2 units will make the function g(x)

`g(x)=-\sqrt{(1)/(3) x}+2`

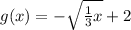
So, the transformed function will be:
`\mathbf{g(x)=-\sqrt{(1)/(3) x}+2}`