Question

`(d)/(dx) \int t^2+1 \ dt`

There is a 2x on the bottom and x^2 on top of the integral symbol
Please help me my teacher did not teach us this:(

Answer 1

`\displaystyle{(d)/(dx) \int \limits_(2x)^(x^2) t^2+1 \ \text{dt} \ = \ 2x^5-8x^2+2x-2`

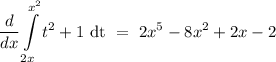
Explanation:

`\displaystyle{(d)/(dx) \int \limits_(2x)^(x^2) t^2+1 \ \text{dt} = \ ?`

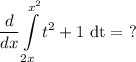
We can use Part I of the Fundamental Theorem of Calculus:

• 
  `\displaystyle(d)/(dx) \int\limits^x_a \text{f(t) dt = f(x)}`

Since we have two functions as the limits of integration, we can use one of the properties of integrals; the additivity rule.

The Additivity Rule for Integrals states that:

• 
  `\displaystyle\int\limits^b_a \text{f(t) dt} + \int\limits^c_b \text{f(t) dt} = \int\limits^c_a \text{f(t) dt}`

We can use this backward and break the integral into two parts. We can use any number for "b", but I will use 0 since it tends to make calculations simpler.

• 
  `\displaystyle (d)/(dx) \int\limits^0_(2x) t^2+1 \text{ dt} \ + \ (d)/(dx) \int\limits^(x^2)_0 t^2+1 \text{ dt}`

We want the variable to be the top limit of integration, so we can use the Order of Integration Rule to rewrite this.

The Order of Integration Rule states that:

• 
  `\displaystyle\int\limits^b_a \text{f(t) dt}\ = -\int\limits^a_b \text{f(t) dt}`

We can use this rule to our advantage by flipping the limits of integration on the first integral and adding a negative sign.

• 
  `\displaystyle (d)/(dx) -\int\limits^(2x)_(0) t^2+1 \text{ dt} \ + \ (d)/(dx) \int\limits^(x^2)_0 t^2+1 \text{ dt}`

Now we can take the derivative of the integrals by using the Fundamental Theorem of Calculus.

When taking the derivative of an integral, we can follow this notation:

• 
  `\displaystyle (d)/(dx) \int\limits^u_a \text{f(t) dt} = \text{f(u)} \cdot (d)/(dx) [u]`
• where u represents any function other than a variable

For the first term, replace
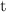`\text{t}` with
`2x`, and apply the chain rule to the function. Do the same for the second term; replace

• 
  `\displaystyle-[(2x)^2+1] \cdot (2) \ + \ [(x^2)^2 + 1] \cdot (2x)`

Simplify the expression by distributing
`2` and
`2x` inside their respective parentheses.

• 
  `[-(8x^2 +2)] + (2x^5 + 2x)`
• 
  `-8x^2 -2 + 2x^5 + 2x`

Rearrange the terms to be in order from the highest degree to the lowest degree.

• 
  `\displaystyle2x^5-8x^2+2x-2`

This is the derivative of the given integral, and thus the solution to the problem.