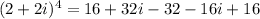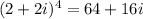Question

If Z= 2+2i, what is z^4?

Answer 1

To find z^4, we can use the binomial theorem or direct multiplication. Using the binomial theorem, we simplify
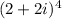`(2 + 2i)^4` to find the result 64 + 16i.

Step-by-step explanation:

To find
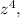`z^4,` we need to raise the complex number z = 2 + 2i to the power of 4. We can do this by using the binomial theorem or by direct multiplication.

Using the binomial theorem, we have:

`(2 + 2i)^4 = C(4,0)(2)^4(2i)^0 + C(4,1)(2)^3(2i)^1 + C(4,2)(2)^2(2i)^2 + C(4,3)(2)^1(2i)^3 + C(4,4)(2)^0(2i)^4`

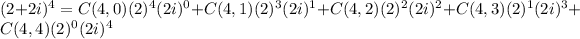
After simplifying and performing the calculations, we get:

`(2 + 2i)^4 = 16 + 32i + 32i^2 + 16i^3 + 16i^4`

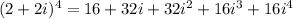
Simplifying further, we obtain:

`(2 + 2i)^4 = 16 + 32i - 32 - 16i + 16`

`(2 + 2i)^4 = 64 + 16i`

Answer 2

D. 64 (cos(pi)+isin(pi))

Step-by-step explanation:

Put 2+2i into trigonometric form, raise the r value to the power of 4, and multiply the angle value (theta) by 4 to get the equation of z^4. In this case, r was 2(sqrt2), which raised to the 4th power was 64. The angle value was pi/4, which multiplied by 4 was pi. That's how we get the answer:

64 (cos(pi)+isin(pi)). How this helps!