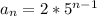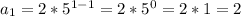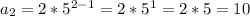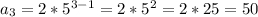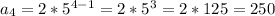Answer:
second term: 10
third term: 50
Explanation:
The equation for any geometric sequence is
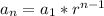 where n is the term number you want to find,
where n is the term number you want to find,
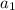 is the first term in the sequence, and
is the first term in the sequence, and
 is the common ratio. The equation for this sequence specifically uses 5 as its common ratio, so the equation is
is the common ratio. The equation for this sequence specifically uses 5 as its common ratio, so the equation is