Answer:
x = A cos (w \sqrt{2y_{o}/g})
a) maximun Ф= \sqrt{\frac{2}{3} \frac{2 y_{o} }{g} }
b) minimun Ф =
 - \sqrt{\frac{2}{3} \frac{2 y_{o} }{g} }
- \sqrt{\frac{2}{3} \frac{2 y_{o} }{g} }
Step-by-step explanation:
For this exercise let's use kinematics to find the time it takes for the mass to reach the floor
y = y₀ + v₀ t - ½ g t²
as the mass is released from rest, its initial velocity is zero (vo = 0) and its height upon reaching the ground is zero (y = 0)
0 = y₀ - ½ g t²
t =

The bucket-spring system has a simple harmonic motion, which is described by
x = A cos wt
in this expression we assumed that the phase constant (Ф) is zero
let's replace the time
x = A cos (w \sqrt{2y_{o}/g})
this is the distance where the system must be for the mass to fall into it.
a) The new system has a total mass of m ’= 3.0 kg, so its angular velocity changes
w =
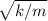
In the initial state
w = \sqrt{k/2}
When the mass changes
w ’= \sqrt{k/3}
the displacement in each case is
x = A cos (wt)
for the new case
x ’= A cos (w’t + Ф)
the phase constant is included to take into account possible changes due to the collision of the mass.
we see that this maximum expressions when the cosine is maximum
cos (w´t + Ф) = 1
w’t + Ф = 0
Ф = -w ’t
Ф = -
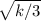

\sqrt{\frac{2}{3} \frac{2 y_{o} }{g} }
b) the function is minimun if
cos (w’t + fi) = 0
w’t + Ф = π / 2
Ф = π / 2 - w ’t
Ф =
 - \sqrt{\frac{2}{3} \frac{2 y_{o} }{g} }
- \sqrt{\frac{2}{3} \frac{2 y_{o} }{g} }