Answer:
The radius of the circle made by the person on the merry go round is 74.55 meters
Step-by-step explanation:
The given parameters are;
The force the merry go round exerts on the rider = 1000 N
The time it takes the merry go round to make one complete revolution = 15 seconds
The weight of the person = 750 N
The radius of the circle made by the person on the merry go round = r
We have;
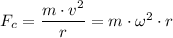
Where;
m = The mass of the person
v = The velocity of the person
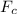 = The centrifugal force acting on the person = 1,000 N
= The centrifugal force acting on the person = 1,000 N
r = The radius of the circle made by the person on the merry go round
ω = Angular velocity = 2·π/15 rad/s
We have;
The mass of the person = The weight/(The acceleration due to gravity, g)
∴ The mass of the person = 750/9.81 ≈ 76.45 kg
By substituting the calculated and known values into the equation for the centripetal force, we have;
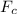 = m × ω² × r
= m × ω² × r
1000 = 76.45 × (2·π/15)² × r
r = 1000/(76.45 × (2·π/15)²) = 74.55 m
The radius of the circle made by the person on the merry go round = r = 74.55 m.