Question

The graph of f (x) = x + 5 is a vertical translation 5 units

up of the graph of f(x) = x. How can you obtain the graph of
f(x) = x + 5 from the graph of f (x) = x using a horizontal
translation?

Answer 1

Graph f(x) = |x - 5|

Answer 2

A horizontal translation of 5 units to the left.

Explanation:

Given the parent linear function:

`\displaystyle f(x)=x`

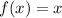
To shift vertically n units, we can simply add n to our function. Hence:

`f(x)=x+n`

So, a vertical shift of 5 units up implies that n=5. So:

`f(x)=x+5`

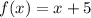
As given.

However, to shift a linear function horizontally, we substitute our x for (x-n), where n is the horizontal shift. So:

`f(x-n)=(x-n)`

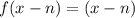
Where n is the horizontal shift.

For example, if we shift our parent linear function 1 unit to the right, this means that n=1. Therefore, our new function will be:

`f(x-1)=(x-1)`

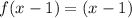
Or:

`f(x)=x-1`

We notice that this is also a vertical shift of 1 unit downwards.

Therefore, we want a number n such that -n=5.

So, n=-5.

Therefore, it we shift our function 5 units to the left, then n=-5.

Then, our function will be:

`f(x-(-5))=(x+5)\text{ or } f(x)=x+5`

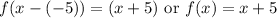
Hence, we can achieve f(x)=x+5 from f(x)=x using a horizontal translation by translating our function 5 units to the left.