Question

The flux through the coils of a solenoid changes from 2.57.10-5 Wb to 9.44.10-5 Wb in 0.0154 s. If 4.08 V of EMF is generated, how many loops does the solenoid have? (No unit)​

Answer 1

Hello!

We can use Faraday's Law of Electromagnetic Induction to solve.

`\epsilon = -N (d\Phi_B)/(dt)`

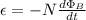
ε = Induced emf (4.08 V)
N = Number of loops (?)

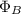`\Phi_B` = Magnetic Flux (Wb)
t = time (s)

**Note: The negative sign can be disregarded for this situation. The sign simply shows how the induced emf OPPOSES the current.

Now, we know that
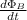`(d\Phi_B)/(dt)` is analogous to the change in magnetic flux over change in time, or
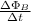`(\Delta \Phi_B)/(\Delta t)`, so:

`\epsilon = N (\Delta \Phi_B)/(\Delta t)\\\\\epsilon = N (\Phi_(Bf) - \Phi_(Bi))/(\Delta t)`

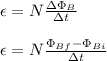
Rearrange the equation to solve for 'N'.

`N = (\epsilon)/( (\Phi_(Bf) - \Phi_(Bi))/(\Delta t))`

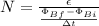
Plug in the given values to solve.

`N = (4.08)/( (9.44*10^(-5) - 2.57*10^(-5))/(0.0154)) = 914.585 = \boxed{915 \text{ coils}}`

**Rounding up because we cannot have a part of a loop.