Answer:
(c) x = 2 and x = -8
Explanation:
The rules of logarithms let you rewrite this as a quadratic equation. That equation will have two (2) potential solutions. We know from the domain of the log function that any negative value of x will be an extraneous solution.
__
The rules of logarithms that apply are ...
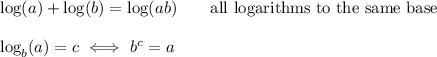
__
take antilogs
We can rewrite the equation so that only one logarithm is involved. Then we can take antilogs.
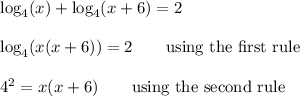
__
solve the quadratic
Adding (6/2)² = 9 to both sides will "complete the square."
16 +9 = x² +6x +9 . . . . . . . add 9
25 = (x +3)²
±√25 = x +3 = ±5 . . . . . take the square root(s)
x = -3 ±5 = {-8, +2}
The two potential solutions are x = 2 and x = -8.