Answer:
(-7/9)^4 = 2401/6561
Explanation:
The rules of exponents apply.
(a^b)/(a^c) = a^(b-c) . . . . . quotient rule
(a^b)^c = a^(bc) . . . . . . . . power rule
__
value of a/b
The first rule of exponents shown above helps us find the value of a/b.

value of (a/b)^2
The second rule of exponents shown above tells us how to find the square.
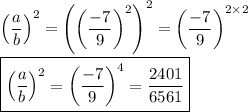
_____
Additional comment
Since -7 is always to an even power in these expressions, its sign can be ignored. The product of an even number of negative values is positive.