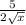Question

use the defintion of the derivative to find the derivative of the given function. f(x)= 5 square root of x

Answer 1

The derivative of function
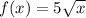`f(x)=5√(x)` is
`(5)/(2√(x) )`

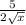
Explanation:

We need to find derivative of the given function
`f(x)=5√(x)`

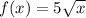
Finding the derivative:

`(d)/(dx)(5√(x) )`

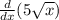
Using the rule (a.f)' = a(f)', taking out constant value 5

`=5(d)/(dx)(√(x) )`

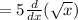
We know
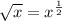`√(x) =x^{(1)/(2)` Replacing
`√(x)`

`=5(d)/(dx)(x^{(1)/(2)} )`

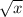
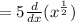
Applying derivative rule:
`(d)/(dx)(x^a)= a.x^(a-1)`

`=5*(1)/(2)(x^{(1)/(2)-1} )\\=(5)/(2)(x^{-(1)/(2)} )\\=\frac{5}{2x^{(1)/(2)}}\\=(5)/(2√(x) )`

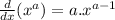
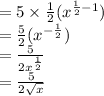
So, the derivative of function
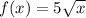`f(x)=5√(x)` is
`(5)/(2√(x) )`