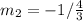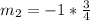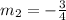Answer:
1. Slope:
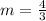
2. Distance:
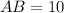
3. Midpoint:
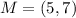
4. Slope of perpendicular line:
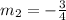
Explanation:
Given
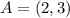
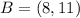
Solving (1): Slope of AB
Slope (m) is calculated as follows:

Where:
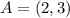 ---
---

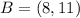 ---
---

So, we have:
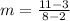
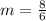
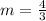
Solving (2): Length AB
This is solved by calculating the distance of AB using the following formula.
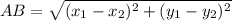
Where:
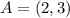 ---
---

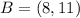 ---
---

So:
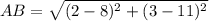
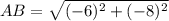
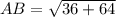
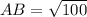
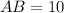
Solving (3): Midpoint of AB.
Midpoint, M is calculated as follows:
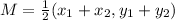
Where
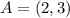 ---
---

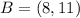 ---
---

So:
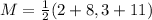
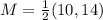
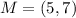
Solving (4): Slope of line perpendicular to AB
The relationship between the slopes of two perpendicular lines is:
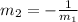
Where
 represents the slope of AB
represents the slope of AB
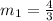
So: