Answer:
AC = 0.47 mi
BC = 0.51 mi
Explanation:
Notice that we are in the case of an acute triangle for which we know two angles ( < A = 63 and < B = 56) and one side (AB = 0.5).
We can find the measure of the third angle using the property of addition of three internal angles of a triangle:
< A + < B + < C = 180
63 + 56 + < C = 180 degrees
< C = 180 - 63 - 56 = 61 degrees.
Now we use the law of sines to find the length of sides AC and BC:

which can be rounded to two decimals as:
AC = 0.47mi
For side BC we use:
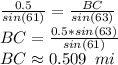
which can be rounded to two decimals as:
BC = 0.51 mi