Question

Circumference of circle T is 4 times the circumference of circle S

Answer 1

Circumference of S = T/4

I didn't quite catch your question though, could you elaborate a bit more?

Answer 2

The radius of circle T is twice the radius of circle S. The circumference of circle T is four times the circumference of circle S. Mathematically, if
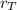`\(r_T\)` is the radius of circle T and
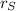`\(r_S\)` is the radius of circle S, then
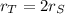`\(r_T = 2r_S\)` and
`\(C_T = 4C_S\).`

Explanation:

In this scenario, the relationship between the two circles, T and S, is established based on their circumferences and radii. The formula for the circumference of a circle,
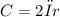`\(C = 2πr\)`, where
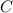`\(C\)` is the circumference and
`\(r\)` is the radius, is utilized.

The given information asserts that the circumference of circle T
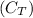`(\(C_T\))` is four times that of circle S
`(\(C_S\))`, expressed as
`\(C_T = 4C_S\)`. By substituting the circumference formula,
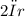`\(2πr\)`, into this relationship, the radius of circle T
`(\(r_T\))` is found to be twice the radius of circle S
`(\(r_S\)`), denoted as
`\(r_T = 2r_S\).`

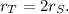
In essence, the radii of the circles follow a simple proportion, where the radius of T is double that of S. This relationship is fundamental to understanding the scaling between the two circles. Consequently, the circumferences are also related by a factor of four, emphasizing the direct proportionality between the radii and circumferences of circles T and S in this mathematical context.