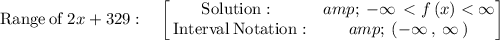Answer:
The range of 2x+329:
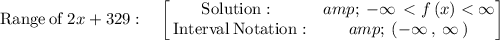
Explanation:
Given the expression
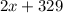
We know that range is termed as the set of values of the dependent variable for which a function is defined.
- We also know that the range of polynomials with odd degree is all the real numbers.
i.e.
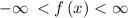
The given expression is a polynomial with an odd degree. Hence, the range of this expression will be all the real numbers.
Thus, the range of 2x+329: