Question

The coordinates of the vertices of a rectangle are (-4, 3), (-1, 5),(3, – 1), and (0, – 3).

What is the perimeter of the rectangle? Round each step to the nearest tenth.
Enter your answer as a decimal in the box.
units

Answer 1

Perimeter of rectangle is 23.34

Explanation:

The coordinates of the vertices of a rectangle are (-4, 3), (-1, 5),(3, – 1), and (0, – 3).

What is the perimeter of the rectangle?

The formula to find perimeter of rectangle is:
`Perimeter=2(l+w)`

We need to find length and width first using the coordinates (-4, 3), (-1, 5),(3, – 1), and (0, – 3).

Let A=(-4, 3) B=(-1, 5) C=(3, – 1) and D=(0, – 3) according to the figure attached.

So, If we find distance of point AB it can be considered length of rectangle and distance of point AC can be considered width of rectangle

The formula used to find distance is:
`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

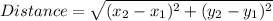
Finding distance AB, we have
`x_1=-4, y_1=3, x_2=-1, y_2=5`

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)\\Distance=√((-1-(-4))^2+(5-3)^2)\\Distance=√((-1+4)^2+(5-3)^2)\\Distance=√((3)^2+(2)^2)\\Distance=√(9+4)\\Distance=√(13)\\Distance=3.61`

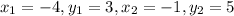
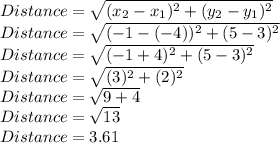
So distance between point A and B is 3.61

Finding distance AC, we have
`x_1=-4, y_1=3, x_2=3, y_2=-1`

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)\\Distance=√((3-(-4))^2+(-1-3)^2)\\Distance=√((3+4)^2+(-1-3)^2) \\Distance=√((7)^2+(-4)^2) \\Distance=√(49+16) \\Distance=√(65)\\Distance=8.06`

So, distance between point A and C is 8.06

We have length = 3.61 and width = 8.06

Using formula of perimeter

`Perimeter=2(l+w)\\Perimeter=2(3.61+8.06)\\Perimeter=2(11.67)\\Perimeter=23.34`

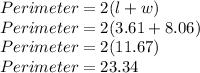
So, Perimeter of rectangle is 23.34