Question

Please help me with this math!

Answer 1

Please check the explanation.

Explanation:

Given the polynomial function

`f\left(x\right)\:=x^3+2x^2-16x-32`

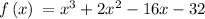
Let us determine the factors by solving

`\:\left0\right\:=x^3+2x^2-16x-32\:`

`\left(x+2\right)\left(x+4\right)\left(x-4\right)=0`

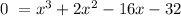
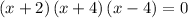
Using the zero factor principle:

if
`ab=0\:\mathrm{then}\:a=0\:\mathrm{or}\:b=0\:\left(\mathrm{or\:both}\:a=0\:\mathrm{and}\:b=0\right)`

`x+2=0\quad \mathrm{or}\quad \:x+4=0\quad \mathrm{or}\quad \:x-4=0`

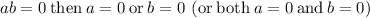
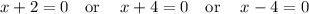
Thus, (x+2) (x+4) and (x-4) are the factors of the polynomial function.

Therefore,

YES

• (x+2)

• (x+4)

• (x-4)

And (x-2) (x+6) are not the factors of the polynomial function.

Therefore,

YES

• (x-2)
• (x+6)