Question

6. Write an equation for the line that is parallel to the given line and that passes through the given point.

3
y =
X-9; (-8. -18)
3
11
y-Ž**ZH
y-
**-12
F
y = $x-12
y=-x+12
G
J

Answer 1

The equation of new line is:
`\mathbf{y=(3)/(4)x-12}`

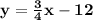
Option H is correct.

Explanation:

We need to write an equation for the line that is parallel to the given line
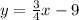`y=(3)/(4) x-9` and point (-8,-18)

The equation of required line will in in form
`y=mx+b` where m is slope and b is y-intercept.

We need to find slope m and b y-intercept for new line.

Finding slope:

When two lines are parallel, they have the same slope.

The slope of given line can be found by comparing the equation
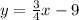`y=(3)/(4) x-9` with
`y=mx+b`

So, m = 3/4

The slope of new line will be:
`m=(3)/(4)`

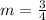
Finding y-intercept:

Using slope m = 3/4 and point (-8,-18) we can find y-intercept

`y=mx+b\\-18=(3)/(4)(-8)+b\\-18=-6+b\\b=-18+6\\b=-12`

So, y-intercept is b=-12

The equation of new line having m = 3/4 and b=-12 is:

`y=mx+b\\y=(3)/(4)x-12`

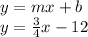
So, the equation of new line is:
`\mathbf{y=(3)/(4)x-12}`

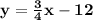
Option H is correct.