Answer:
The approximate speed of the object when it hits the ground is 63.568 meters per second.
Step-by-step explanation:
The height of the object launched vertically upward is represented by the function
 . The approximate speed of the object when it hits the ground occurs when
. The approximate speed of the object when it hits the ground occurs when
 . Then, we solve the resulting second-order polynomial by the Quadratic Formula:
. Then, we solve the resulting second-order polynomial by the Quadratic Formula:
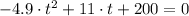 (1)
(1)
The roots associated to this polynomial are, respectively:
 and
and
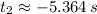
Given that time is a positive variable, the only solution that is physically reasonable is:
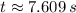
The function velocity is the first derivative of the function defined at the commencement of the explanation, that is:
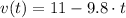 (2)
(2)
If we know that
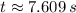 , then the approximate velocity of the object when it hits the ground is:
, then the approximate velocity of the object when it hits the ground is:
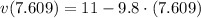
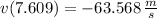
The speed is the magnitude of this velocity. Therefore, the approximate speed of the object when it hits the ground is 63.568 meters per second.