Answer:
11.7 (3 s.f.)
Explanation:
Given information:
- ∠CAB = 90°
- ∠ABC = 52°
- AC = 9.2
As one of the given angles is 90°, the triangle is a right triangle.
Draw the triangle using the given information (see attached) to help visualize the problem.
To calculate the length of BC, use the sine trigonometric ratio:
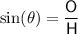
where:
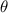 is the angle
is the angle- O is the side opposite the angle
- H is the hypotenuse (the side opposite the right angle)
From inspection of the attached triangle:
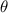 = 52°
= 52°- O = AC = 9.2
- H = BC
Substitute the values into the formula and solve for BC:
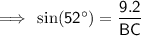
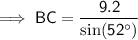
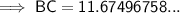
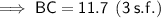
Therefore, the length of BC is 11.7 (3 s.f.).