Answer:
The change in kinetic energy of the car is -189434 joules.
The work done by the car is 189434 joules.
The magnitude of the force that pushed the front of the car is 498510.526 newtons.
Step-by-step explanation:
Given that the car is moving on a horizontal ground, by the Principle of Energy Conservation and the Work-Energy Theorem we get the following identity:
 (1)
(1)
Where:
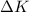 - Change in the translational kinetic energy of the car, measured in joules.
- Change in the translational kinetic energy of the car, measured in joules.
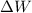 - Work done by the car, measured in joules.
- Work done by the car, measured in joules.
By applying the defintions of translational kinetic energy and work, we expand and simplify the resulting equation:
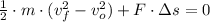 (2)
(2)
Where:
 - Mass, measured in kilograms.
- Mass, measured in kilograms.
 ,
,
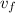 - Initial and final speeds of the car, measured in meters per second.
- Initial and final speeds of the car, measured in meters per second.
 - Force exerted by the car, measured in newtons.
- Force exerted by the car, measured in newtons.
 - Travelled distance of the front of the car, measured in meters.
- Travelled distance of the front of the car, measured in meters.
The change in the kinetic energy of the car and the work done by the car are, respectively:
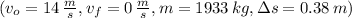
Translational kinetic energy
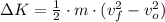
![\Delta K = (1)/(2)\cdot (1933\,kg)\cdot \left[\left(0\,(m)/(s) \right)^(2)-\left(14\,(m)/(s) \right)^(2)\right]](https://img.qammunity.org/2021/formulas/physics/high-school/jmikuhvpxhk1x6mzorxycovf1s9y6egg8c.png)
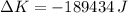
Work done by the car
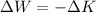
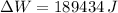
Magnitude of the force
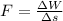
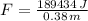
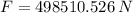
The change in kinetic energy of the car is -189434 joules.
The work done by the car is 189434 joules.
The magnitude of the force that pushed the front of the car is 498510.526 newtons.