Question

A line segment AB has the coordinates A (2,3) AND B ( 8,11) answer the following questions (1) What is the slope of AB? (2) What is the length of AB? (3) What are the coordinates of the mid point of AB?(4) What is the slope of a line perpendicular to AB ?

Answer 1

(1) The slope of the line segment AB is 1.
`\bar 3`

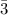
(2) The length of the line segment AB is 10

(3) The coordinates of the midpoint of AB is (5, 7)

(4) The slope of a line perpendicular to the line AB is-0.75

Explanation:

The coordinates of the line segment AB are;

A(2, 3) and B(8, 11)

(1) The slope of a line segment is given by the following equation;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

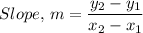
Where;

(x₁, y₁) and (x₂, y₂) are two points on the line segment

Therefore;

The slope, m, of the line segment AB is given as follows;

A(2, 3) = (x₁, y₁) and B(8, 11) = (x₂, y₂)

`Slope, \, m_(AB) =(11-3)/(8-2) = (8)/(6) = 1 (1)/(3) = 1.\bar3`

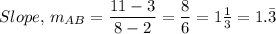
The slope of the line segment AB = 1.
`\bar 3`

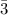
(2) The length, l, of the line segment AB is given by the following equation;

`l = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}`

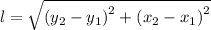
Therefore, we have;

`l_(AB) = \sqrt{\left (11-3 \right )^(2)+\left (8-2 \right )^(2)} = √(64 +36) = 10`

The length of the line segment AB is 10

(3) The coordinates of the midpoint of AB is given as follows;

`Midpoint, M = \left ((x_1 + x_2)/(2) , \ (y_1 + y_2)/(2) \right )`

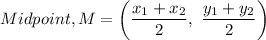
Therefore;

`Midpoint, M_(AB) = \left ((2 + 8)/(2) , \ (3 + 11)/(2) \right ) = (5, \ 7)`

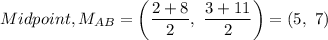
The coordinates of the midpoint of AB is (5, 7)

(4) The relationship between the slope, m₁, of a line AB perpendicular to another line DE with slope m₂, is given as follows;

`m_1 = -(1)/(m_2)`

Therefore, the slope, m₁, of the line perpendicular to the line AB, that has a slope m₂ = 4/3 = 1.
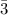`\bar 3` is given as follows;

`m_1 = -\left ((1)/((4)/(3) ) \right ) = -(3)/(4) = -0.75`

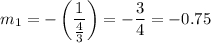
The slope, m₁, of the line perpendicular to the line AB is m₁ = -0.75.